What is calculus and what is it used for? Calculus includes an enormous number of ideas, methods, and applications, and this post is an attempt to provide an overview.
Most of the interesting phenomena that are analyzed scientifically involve change. The flow of wind and water, the orbits of the planets, the path of a baseball, the movement of a shark, the decay of a pile of leaves, the digestion of food, the growth of a child — all are situations involving change. In any change situation, one of the most important questions is: What is the rate of change? That is, how fast is the change occurring? One aspect of calculus (differential calculus) addresses such questions.
Most quantities of interest in science are modelled by continuous functions. Differential calculus can be considered to be a tool for analyzing continuous functions. Besides the class of applications mentioned in the previous paragraph, calculus is therefore also useful in pure mathematics.
The graph of a function provides a very useful visual representation of the function. For a straight-line graph of a function of time, the slope of the graph represents the rate of change of the quantity modelled by the function. Thus, the slope of a graph is of key importance in applications. However, how does one determine the slope of the graph of a function that is not a straight line? This is the key question addressed by differential calculus.
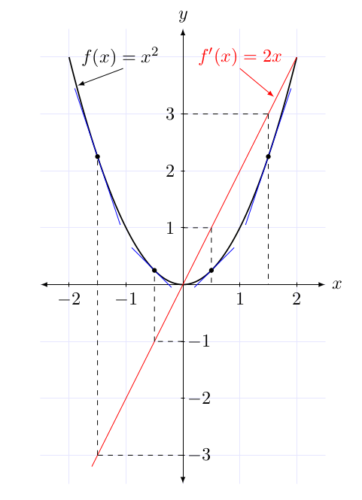
Thus, we have a connected set of concepts: Rate of change is a scientifically useful quantity, which is related to the slope of the graph of the function that models the quantity, which can be calculated by an algebraic procedure. The algebraic procedure results in another function, related to the original function, called the derivative of the original function, which contains all the information about the rate of change of the original function. The process by which one obtains the derivative from the original function is called differentiation, and is based on the concept of the limit of a function. All of these concepts will be explained in detail in the textbook posted at the web site, but at least you are now acquainted with the names of these important concepts. The basic derivative concept is illustrated for an example function in the figure below, where the dark curve is the graph of a function and the red line is the graph of its derivative function. Don’t worry if you don’t understand the figure yet; we’ll explain it in detail at the textbook page. For now, just contemplate the figure and see what you can extract from it.
Calculus is a Latin word that means small stone. In ancient times small stones were used as an aid to counting. The word calculate derives from this usage of the word. In medicine, a calculus is a mineral deposit in the body, such as a kidney stone. As mathematics developed, several different systems for calculating various quantities were developed, and these are all called some kind of calculus, as you will learn if you progress far enough in your mathematics studies. What we now call calculus used to be called infinitesimal calculus as a way to distinguish it from other systems of calculation. However, over time, laziness has resulted in “infinitesimal” being dropped, and so it is now universally known as calculus. As you learn about limits at the very beginning of your calculus studies, you will understand what the “infinitesimal” has to do with the subject.
Differential calculus is almost universally learned first, but the more challenging integral calculus is even more important and practical in applications. The purpose of differential calculus is to analyze functions to determine their properties, including their rates of change. An important basic purpose of integral calculus is to determine the total accumulated amount of a quantity that gradually changes.
For example, if you have money in your bank account or in an investment that earns interest every month, there is no need to use calculus to determine the total value of your investment at the end of a year. You simply take the initial value of the investment and add the twelve interest quantities that were earned at the end of each month. If every second two drops of water fall from a water tap, after $100$ seconds a total of $2 \times 100 = 200$ drops of water will have fallen. No calculus needed.
However, consider a ball that you drop out of a tall building. The ball will gradually pick up speed at a certain rate. What is the ball’s speed after $2.4$ seconds? Well, that’s a more challenging problem than the investment and droplet problems in the previous paragraph, which were discrete. The problem of the falling ball is a continuous one; the ball’s speed increases gradually and continuously. This is a problem for integral calculus, although in the simple situation of no air resistance, one can calculate the result readily without using the full power of integral calculus, as we shall see.
The acceleration function of the ball is the derivative of the ball’s velocity function. We can rely on various experiments to help us determine the acceleration function of the ball. What we seek is the value of the velocity function of the ball after $2.4$ seconds. In this context, we can refer to the velocity function as the anti-derivative of the acceleration function. The process of determining the velocity function from the given acceleration function is called anti-differentiation, or, equivalently, integration.
So, to summarize the differences between differential and integral calculus:
Differential calculus: You have a function of time that models a quantity. The derivative of the function tells you the rate of change of the quantity.
Integral calculus: You have a function that models the rate of change of a quantity in time. The anti-derivative of the function tells you the accumulated amount of the quantity after some time has passed.
Phrased in this way, you can see that the basic problems of differential calculus and integral calculus are sort of inverses of each other. In differential calculus you seek the derivative of a function to help you analyze it. In integral calculus problems, you know the derivative function, and you seek the original function, or at least a certain value of the original function.
Just as the basic problem of differential calculus as a geometric exemplar (calculating the slope of a curve), so does the basic problem of integral calculus, which will now be described. We humans have enormous visual cortexes in our brains, and so visual representations are a great aid to learning. Therefore many concepts in mathematics are first presented as geometric or other visual problems, so that they will be as memorable as possible, even though their most general applications typically go far beyond the simple visual situations we first use to explain the concepts.
Suppose that you have the graph of a function and you wish to determine the area enclosed by the graph, the horizontal axis, and two vertical lines. This is indicated by the shaded region labelled “S” in the following figure.
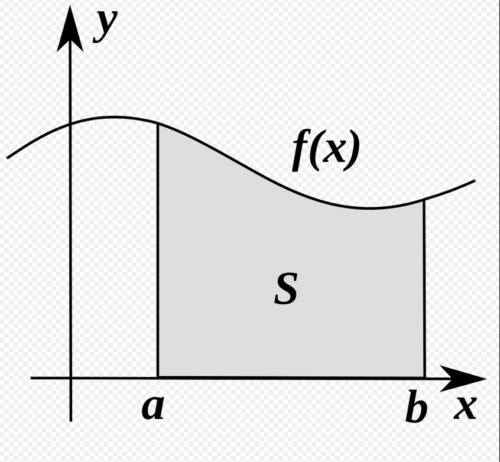
Suppose that the graph represents the acceleration of a falling object plotted against time. It is a fact that the area of the shaded region then represents the change in the object’s velocity between the times $a$ and $b$. Thus, the problem of determining the change in the object’s velocity has been reduced to a geometric problem, and this kind of graph is useful in developing the basic concepts and techniques of integral calculus. Once the techniques have been understood, they are applicable to other situations beyond the original graph.
For example, suppose that you are an engineer designing a propulsion system for sending a space craft to the Moon. You will first have to determine the position of the Moon at all future times. You can do this using Newtonian mechanics, one of the best and most useful physical theories available. In particular, you would use Newton’s second law of motion,
$$
\vec{F} = m\vec{a}
$$
which can also be written as
$$
\vec{a} = \dfrac{\vec{F}}{m}
$$
In applying Newton’s law of motion, you focus your attention on the Moon. You then add up all of the forces acting on the Moon at this moment as vectors, and then divide by the mass of the Moon. (The forces acting on the Moon are gravitational forces exerted by the Sun, the Earth, other planets, and so on.) The result is a vector that tells you the magnitude and direction of the acceleration of the Moon right now. Knowing the position of the velocity of the Moon right now, you can then predict what the position of the Moon will be a fraction of a second from now. But by then the positions of the Moon, the Sun, the Earth, and the rest of the planets will have changed, so you will have to re-do the calculation to determine where the Moon will be a fraction of a second later. This is the kind of calculation that you can automate using an electronic computer, but you will have to understand the situation thoroughly so that you can program the computer correctly.
In summary, careful measurements can give you the current position and velocity of the Moon, and the positions of all of the other planets. Then you use Newton’s law of gravity to determine the magnitudes and directions of all the forces acting on the Moon. Then you add up all of the forces as vectors and then apply Newton’s second law of motion to determine the Moon’s acceleration. The you use calculus to determine the Moon’s subsequent velocity and subsequent position. The process here is like the process of anti-differentiation (integration) as described earlier.
Once you know the Moon’s location at all future times (i.e., you know the Moon’s position function), you will be able to plan how to propel your space craft so that it will reach the Moon gently and safely at the right time and place.
The same sort of problem-solving procedure occurs in many different fields of science. Newton’s second law of motion can be considered to be a differential equation, because it is a relation involving a quantity of interest (position), its derivatives, and perhaps other quantities. In the Moon example, it is the position function of the Moon that is of main interest, but Newton’s second law of motion involves the second derivative of the position function. One has to differentiate the position function to obtain the velocity function, then differentiate the velocity function to obtain the acceleration function. Two differentiations are needed to go from position function to acceleration function. For this reason, Newton’s second law of motion is said to be a second-order differential equation for the position function.
Many of the most important quantities in physics, engineering, and other scientific fields satisfy differential equations, and many of them are second-order differential equations. Thus, gaining a deep understanding of physics, engineering, and many other fields of science, requires an understanding of differential equations and how to solve them. Once you understand integral calculus you will be able to build on this to start tackling differential equations.
The subject of differential equations can therefore be considered to be an advanced branch of calculus. The usual sequence of learning is that you first learn about “single-variable” calculus; that is, you learn how to apply calculus tools to functions of one variable, which are the kind you can plot on graph paper. Then you can learn about differential equations, and at the same time learn about applying calculus to functions of several variables; the latter is called multi-variable calculus, and also vector calculus.
In the overall scheme of mathematics, calculus, vector calculus, and differential equations lie on a branch of mathematics called real analysis. There are other branches of analysis, such as complex analysis, functional analysis, numerical analysis, and you might also consider probability and statistics to be in this category as well. Taking a wider view to include other branches of mathematics, the three1 pillars of mathematics are analysis, topology, algebra, and combinatorics.2 Combinatorics is the systematic study of counting techniques; counting a small number of things can be easy, but counting all possible ways that various things can occur can be very difficult, and ingenious techniques have been dreamed up to cope with these difficulties. Topology is concerned with the shapes of various kinds of geometrical objects, and the shapes of various kinds of mathematical spaces, and in particular which kinds of properties of geometrical objects are invariant with respect to continuous deformations. Algebra, broadly speaking, deals with structural matters in mathematics, such as identifying interesting mathematical systems to study, and then abstracting the essential properties of the systems so that theorems can be proved about all possible examples that share the same properties. Thus, in advanced algebra, one specifies various systems using axioms (definitions used as starting points), and then one uses logic to prove what one can about all such systems. Algebra is therefore harder for most people to deal with, because of its abstraction, but the rewards are many, for this kind of abstract, structural approach yields many insights that one would not have obtained by studying only concrete examples. However, beginners should learn by careful study of numerous well-chosen examples as a start, and only get into abstractions later. Unfortunately, many university courses in mathematics, particularly at higher levels, are taught too abstractly.
The same spirit of abstraction obtains in the study of mathematical logic and set theory, which lie at the foundations of mathematics. There are other ways to categorize mathematics (pure mathematics vs. applied mathematics, for example), but thinking in terms of the pillars of analysis, algebra, topology, and combinatorics may be helpful for you as you navigate the vast landscape of mathematics.
1. There are three kinds of people in the world: Those who can count and those who can’t count.
2. This is a little joke, as combinatorics still doesn’t get the respect it deserves from some prominent mathematicians, according to some prominent combinatorics practitioners.
