One of the most important tools that mathematicians and scientists use to cope with the daunting complexity of the world goes by the name of reductionism. That is, one first identifies the key parts of a complex system, then one strives to understand the parts, and finally one strives to understand how the parts fit together and interact among themselves.
I’ll focus on this interpretation of reductionism, and ignore another possible interpretation of the word (that a complex system is nothing but the sum of its constituent parts) because I don’t believe the latter to be true.
Reductionism, in the first sense listed above, has been a very successful approach in both mathematics and science. We humans have sometimes pushed the idea too far … often with grave consequences for the biosphere. When we assume that the number of fish in the ocean is infinite, and therefore harvest them in ways that destroy ecosystems (see also here), or wastefully by discarding enormous amounts of “bycatch,” then we are operating over-simplistically. And stupidly. When we introduce a foreign species in an attempt to solve a problem in an ecosystem that ends up causing a lot of unforeseen damage to the ecosystem, then again we are oversimplifying to a stupid degree. In such cases, holistic thinking would be a wise preventive measure.
But in terms of helping us to understand the complexity of the world, reductionism has been a very successful philosophy. In this post we’ll look at a number of examples of reductionism in mathematics; in a subsequent post we’ll consider examples in science.
The concept of a basis in mathematics
I’ve mentioned the concept of a basis in a previous post, and it’s so important that it’s worth discussing in some detail.
In elementary school one learns about number lines, typically starting with whole numbers. A number line is an aid for visualizing addition and subtraction. An interesting feature of a number line is that it extends indefinitely towards the right, which gets us started thinking about infinity and what that concept means (we’ll save a detailed discussion of infinity for another time).
Next, we suppose that the number line extends indefinitely towards the left as well, as a way of visualizing integers.
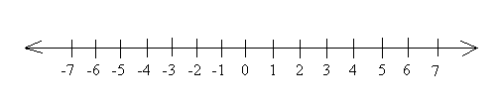
What about the positions on the number line between the tick marks representing whole numbers? Shouldn’t they also represent numbers? Well, yes, they do, and now our strengthened number line ought to be called a real number line, as opposed to the earlier versions, which could be called natural number line and integer number line, respectively.
OK, good, so we now have a real number line, which gives us a geometrical representation of all real numbers. It’s somewhat like a carpenter’s measuring tape, in that it can be applied to describe measures along a line, such as the position of a car along a straight stretch of highway.
However, in describing how quantities evolve in time, it is useful to plot graphs having two axes; that is, two real number lines, at right angles to each other. In this way, we can plot, for example, the position of a car moving along a straight highway as it moves in time. The slope of the graph then gives us a sense for the velocity of the car. And we can plot the evolution in time of any other quantity that can be described by a single real number (such as the balance in your bank account, the value of your house, etc.).
Notice that the frame of the graph with two axes (which we’ll describe as two-dimensional, since it has two axes) was built by pasting together two one-dimensional real number lines. In technical terms, we say that the two-dimensional space upon which we plot a graph is the direct sum of the two one-dimensional real number lines. In symbols, we use $\mathbb{R}$ to represent either of the two real number lines, and then we use $\mathbb{R} \oplus \mathbb{R}$, or $\mathbb{R}^2$ for short, to represent the two-dimensional real space.
Specifying the location of a point in the two-dimensional space $\mathbb{R}^2$ can be done in a number of ways. One way is to use rectangular coördinates: start at the origin of the coördinate system (the point at which the axes cross), then specify how far one has to walk in the “horizontal” direction, and finally specify how far one has to walk in the “vertical” direction to end up at the point in question. By convention, walking “East” or “North” on the graph is described by a positive number, whereas walking “West” or “South” is described by a negative number.
A compact way to represent this process is to just specify a pair of numbers, such as $(2, 3)$. This ordered pair of numbers specifies a point that is $2$ units “East” of the origin and $3$ units “North” of the origin.
Thus, every location in $\mathbb{R}^2$ can be represented by an ordered pair of numbers, and every ordered pair of numbers specifies the location of one and only one location in $\mathbb{R}^2$. We say the collection of points in $\mathbb{R}^2$ (which extends indefinitely in all directions) is in one-to-one correspondence with the collection of all possible ordered pairs with real coördinates.
Now, we can identify two basic movements in getting from the origin to any point in $\mathbb{R}^2$: Moving “East” by one unit, symbolized by $(1, 0)$, and moving “North” by one unit, symbolized by $(0, 1)$. These two basic movements are said to form a basis for $\mathbb{R}^2$, because every location in $\mathbb{R}^2$ can be specified by combining some multiple of each of the basic movements. (In technical terms, we say that each element of $\mathbb{R}^2$ can be expressed as a linear combination of the basis elements $(1, 0)$ and $(0, 1)$.) For example,
$(3.7, –1.4) = 3.1(1, 0) + [–1.4](0, 1)$
I’ve implicitly used the rules for operating with ordered pairs: (1) When multiplying an ordered pair by a factor, multiply each number in the pair by the factor, and (2) When adding two ordered pairs, add the first number in each pair to get the first number of the resulting ordered pair, and add the second number in each pair to get the second number of the resulting ordered pair.
Another graphical way to visualize the combination of basic movements from the origin to reach all possible locations, is to represent the basic movements as arrows. The location of each point in $\mathbb{R}^2$ can also be represented by an arrow that starts at the origin and ends at the point in question.
What we have described for $\mathbb{R}^2$ can also be done in other realms. We can construct higher-dimensional spaces (such as $\mathbb{R}^3$, $\mathbb{R}^4$, and so on), and we can also construct more abstract spaces, which we’ll describe in a subsequent post. Such spaces are examples of what are called vector spaces.
In the next post, we’ll discuss the concept of a basis in an infinite-dimensional space. In a subsequent post, we’ll discuss the analogue of the basis concept in physics/chemistry, which brings us to the story of atoms and their constituents.
* * *
Click here to read Atoms in Mathematics and Science, Part 2: Infinite-Dimensional Spaces.
(This post first appeared at my other (now deleted) blog, and was transferred to this blog on 25 January 2021.)